私たちは、高校や大学において当然のように微分積分学を学んできました。理系の高校生であれば教育課程の数学Ⅲの大部分を微分積分が占めていますし、文系の生徒でも教育課程の数学Ⅱに微分積分が入っているので、少なくとも何らかの形で触れたことがある人が多いのではないかと思います。大学においても理工系学部では、微分積分に全く触れないということは少ないのではないかと思います。
微分積分というのは数学教育においてかなり重要視されてきた分野であると言えると思います。しかし、その微分積分という分野が、もし根底からひっくり返る可能性があると聞いたら、どう思われますか？
「そんなわけない」と思われる方もいらっしゃるかもしれません。とはいえ、RAPT理論によって様々な常識が覆されてきた今、数学・物理学界においても、これまでの常識を覆す発見が成されつつあるとしても不思議ではないでしょう。
◇RAPT×読者対談〈第70弾〉ノーベル賞創設の目的はアインシュタインの嘘を隠蔽するため。
◇RAPT×読者対談〈第99弾〉原発も水素自動車もその燃料はただの水と塩。
微分積分は、連続実数値の関数において、微小差分を無限に０に近づけるという極限の概念を用います。
しかし、ゲーデルの不完全性定理の中枢を成す「再帰的数え上げ」という概念を用いると、どんな連続実数値に対しても無限に近づくことができるのかという問題が生じ、連続実数値の存在すらも危うくなってしまうようです。
ちなみに再帰とは、Wikipediaにはこのように記載されています。
—————————————–（以下こちらより引用）
再帰（さいき、英: Recursion, Recursive）とは、ある物事について記述する際に、記述しているもの自体への参照が[注釈 1]、その記述中にあらわれることをいう。
再帰は言語学から論理学に至る様々な分野で使用されている。最も一般的な適用は数学と計算機科学で、定義されている関数がそれ自身の定義の中で参照利用されている場合を言う。
……
関数での再帰
詳細は「漸化式」を参照
関数は自身を再帰的に定義する場合がある。とりわけ漸化式が数列を再帰的に定める数式であり、その身近な例が
というフィボナッチ数列である。こうした漸化式による定義が成立する場合、その数式は再帰を用いずに定義された基底値 （フィボナッチの場合
と
）に帰着できる必要がある。また、漸化式の再帰関係を解いた場合は非再帰的な定義（一般項）を得ることが可能である[注釈 4]。
——————————————-（引用ここまで）
連続実数値の世界が覆されたなら、その影響は数学界にとどまらず、物理学界にも波及します。また、物理学でもハイゼンベルクの不確定性原理やプランク定数によって、この世の中が連続実数値ではなく離散値で形成されている事実が示唆されています。
———————————————（以下こちらより引用）
[註]
＜以下に私・佐野千遥が述べるのは、全く新しい体系のスミルノフ物理学の数学的基礎論の中枢であり、又、物理学専門でない方々にも非常に容易に理解できる様に、数式をほぼ何も含めないで、証明の趣旨を文章で明記して有りますので、是非最後までお読み下さり、カッコ付「正統派」現代物理学と異なり、スミルノフ物理学は如何に単純明快であるかを実際に御確認下さい。世界史上他の人が誰も言ったり考えたりした事が無い全く新しい事をスミルノフ物理学が言っている為に、一回目に読む時には、取っ付き難（にく）い点は有るかもしれませんが、それは「取っ付き難（にく）さ」であって「難しさ」では全くありません。＞
[註]
＜１万倍の複雑な数式を使った誤謬のカッコ付「正統派」現代物理学とは、大学生はフムフムと言いながら分かったような顔をして読んでいますが、その実、その幾重もの矛盾故に、本当は物理学専門家でも「理解」できる代物ではありません。ノーベル賞受賞者・ファインマンが正直にそう書いています。そのカッコ付「正統派」現代物理学とスミルノフ物理学とは難易度の点で天と地の違いが有ります。つまりスミルノフ物理学は「超簡単」であることを、御理解下さい。数学的に複雑である事は、正しい事を意味しません。而もカッコ付「正統派」現代物理学が使っている複雑な数式は、誤謬の確率論と微積分学ですから、当然数式としても理論としても完全に誤っています。
以下に述べる全く新しい体系のスミルノフ物理学の数学的基礎の単純極まりない明々快々な論旨を把握できない場合、それは脳神経のエネルギー代謝を司る主要必須ミネラルのカルシウムの摂取量不足[日本人は欧米人の４分の１しかカルシウムを摂取していない]が原因である可能性が有ります。＞
以下本論
数学基礎論のゲーデルの不完全性定理の解釈については、色々と哲学的な説明をしている本が出版されていますが、ゲーデルの不完全性定理の証明の中枢はrecursively enumerable（再帰的数え上げ可能性）の概念に基づいています。
結論から先に申しますと、この「再帰的数え上げ可能性」に基づくと、連続実数なるものの数学的存在が証明できなくなります。
例えば、微積分学に於いて、微小差分を０に近付ける極限の概念を
lim の下に ∆x → 0
と書いて表しますが、ここでxはどんな連続実数値でも構わない事に成っています。
つまりどんな連続実数値をもった実数であろうと、必ずその値に無限に接近する事が出来る事を前提にしてしまっています。
ところで、果たして本当に必ず如何なる連続実数値にも無限に接近する事が出来るのでしょうか？
例えば、root (5) = 2.2360679…. に最も近い実数をxとします。このxに∆x → 0のように、無限に接近する事は可能ですか？
答は当然「否」ですね。
つまり有理数でないから、循環小数ではなく、つまり再帰的数え上げ可能でなく、小数点以下で数字0,1,2,3,4,5,6,7,8,9の中のどれが次に出て来るかは、予測が付かない問題が生じます。x軸の数直線上には所狭しとゴッチャ混ぜに“連続実数”なるものが犇（ひし）めき合っているので、連続実数には附番することが出来ない分けです。
ゲーデルはこのように「無限」の概念をもっと厳密に扱わねばならない事を数学会に厳重に警告しているのであって、ゲーデルの不完全性定理に基づき、連続実数なる数は存在証明が出来ない事となり、連続実数なる数は数学者の頭の中にだけ有って、実際の数学の世界には存在しない数という事となります。
依って更に、この存在しない連続実数に基づいて築かれた確率論と微積分学とは、色々数学分野が有る中で、誤った数学分野という事になります。
その結果更に、この誤った数学の確率論と微積分を大幅に取り入れたカッコ付「正統派」現代物理学や経済学が、大混乱の誤謬“科学”に陥るのは理の当然となります。
つまり、数学の世界では有理数に基づく「離散値の数学」分野が正しい数学であり、更に、驚くべき事に、物理学の世界でも２０世紀初頭に、プランク定数、ハイゼンベルクの不確定性原理（カッコ付「正統派」現代物理学によるハイゼンベルクの不確定性原理の確率論的解釈は誤りで、離散値の解釈、有理数値の解釈が正しい）が発見されており、これは物理世界でも離散値の物理学が正しい事を示しています。
このように物理学の世界は数学の世界と地続きであり、共に離散値の概念を逸脱すると誤謬の科学に陥る事が必然であります。
更に論じます。
２０世紀の初頭に、アンリー・ポワンカレーという数理物理学者が、３体以上の多体問題は微積分の方法によっては解けない事を証明しました。
これはもっと平たく言うと、例えば３つ以上の星が互いに重力で引き合いながら運動している時、３つの星の時々刻々の位置を微積分学を使って解く事ができない、という意味です。
これは正に動的作用反作用の問題でしたから、アンリー・ポワンカレーの上記証明を受けて、今日スミルノフ学派がその公理性を主張する「ニュートンの動的作用反作用の法則」を知らないカッコ付「正統派」現代物理学会の論文からは、アンリー・ポワンカレーのこの証明以後、動的作用反作用の現場を捉えた実験式が悉く消滅する事となりました。
ところで２００６年、私・佐野千遥はサンクト・ペテルブルグの物理学会で、
１ アンリー・ポワンカレ―の上で言及した証明は、非常に片手落ちの証明でしか無かった事を述べた。何故なら、アンリ―・ポワンカレ―は微積分が欠陥数学である事を知らずに、その欠陥数学・微積分学を使って、“３体以上の多体問題が解けない。”と論証したにしか過ぎないからである。
ですから、このポワンカレーのこの論証の数学的物理学的背景を調べる事無く、鵜呑みにし、更にはポワンカレーのこの論証を口実に、物理学の中枢であるべき動的作用反作用の論の構築を放棄したカッコ付「正統派」現代物理学は、二重三重多重の自力では脱出不可能な誤謬に嵌（は）まり込む事となりました。
２ 私・佐野千遥は、アンリー・ポワンカレーが連続実数の上に造られた誤った数学の微積分学を使ったから、３体以上の多体問題を解けなかった事を論証した。
物理学の世界、数学の世界は共に離散値の世界であるために、本当は時間軸上に並んだ時刻を表す有理数は飛び飛びにしか存在しないのだから、物理現象の過程は区切る事が可能であり、また作用反作用は２体ずつの間で交わされるのが真実の姿であるのにも拘わらず、例えば３体問題に連続実数に基づく微積分学を適用して解こうとすれば、時間を区切る事無く３元連立微積分方程式を同時に解かなければならなくなる羽目に陥り、それを解く事は当然不可能と成る分けです。
アンリ―・ポワンカレ―はこの当然証明不可能となる微積分学の絡繰りを理解しないまま、３体以上の多体問題を解けない事を誤謬の微積分学を使って導いたにしか過ぎないのだから、彼の為した証明は大した物理学的貢献では全く無いのである。
３ 私・佐野千遥は、物理学の世界、数学の世界は共に離散値の世界であるために、本当は時間軸上に並んだ時刻を表す有理数は飛び飛びにしか存在しないのだから、物理現象の過程は区切る事が可能であり、また作用反作用は２体ずつの間で交わされるのが真実の姿であるので、３体、又は多体間の作用反作用に、有理数時間軸を区切って、２体ずつの動的作用反作用に分け（その今選ばれている２体以外は、その２体が相互作用を交わしている最中は、作用反作用をせずに待っている）、ニュートンの動的作用反作用の法則に離散値の数学である差分・和分学を導入して適用すると、３体であろうが多体であろうが必ず解ける事を論証したのである！！！恩師アナトリー・パーブロビッチ・スミルノフ博士と佐野千遥が組んで実現したこの“多体問題解決可能！”の論証は、物理学会における偉業と言うべきものである事は言を待たない。
以上論証した事から、私・佐野千遥は
１ ゲーデルの不完全性定理と離散値論による現代数学会の解体・刷新
２ カッコ付「正統派」現代物理学会の打倒と、ノーベル賞委員会の解体
を推進しています。
——————————————-（引用ここまで）
このように、物理学に大いに導入されてきた連続実数値による微分積分学の概念が根底から誤りならば、ノーベル賞によって権威付けられてきた”現代物理学”も連鎖的に崩壊するでしょう。私たちは、これまでの常識を完全に捨て去って、数学や科学の新しい枠組みを築き上げていく必要があるのかもしれません。
◇RAPT×読者対談〈第112弾〉現代科学の知識はどこまで本当か。
物理学以外にも、RAPT理論の登場により、さまざまな分野の常識が常識として通用しなくなり、まさに時代の転換を迎えたと言える今、一人でも多くの方々がRAPTブログに出会い、絶対的な真理をもとに困難を乗り越え、大きく発展し、祝福された人生を歩まれますことをお祈り申し上げます。
お読みいただきありがとうございました。
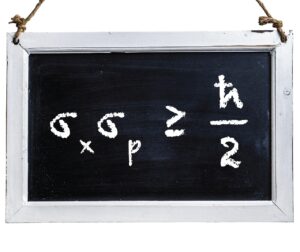
コメント