現代物理学においては、量子力学の発展によって、確率論的な解釈がその大部分で成されてきました。
——————————————–(以下こちらより引用)
量子力学は、このボーアの「相補性」と、波動関数の振幅の二乗が粒子の存在確率になるという「ボルンの確率解釈」、測定そのものが対象の物理状態を乱してしまうことを示した「ハイゼンベルクの不確定性原理」という主に3つの概念に基礎づけられた「コペンハーゲン解釈」によって、前世紀を通じて大きく発展してきました。
——————————————-(引用ここまで)
また、「放射性崩壊」とは、原子核が、α線やγ線などの放射線(電磁波)を放出することで、他の安定な原子核に変化する現象であり、ランダムな確率的な現象として説明されてきました。
——————————————–(以下こちらより引用)
放射壊変はランダムに起こる現象であって、特定の原子に注目するときそれがいつ壊変するかは予言できず、ただある時間間隔Δtに壊変する確率pを知り得るのみである。
——————————————-(引用ここまで)
しかし、予測できない不規則で複雑な現象を説明する方法として、上記のランダムな確率理論の他に、決定論的な力学系によって生み出されるカオス理論という理論があります。力学系とは、初期値が決定すればその後の全ての状態量の変化が決定するという系(システム)のことです。
ランダムでは入力値に対して、出力値はデタラメな値が出てきますが、カオスでは、不規則な出力値ではあるものの、入力値に対して出力値は決定論的に、一意に出力されます。
カオス理論で不規則な複雑さを説明するならば、ランダムな偶然だと解釈するのではなく、原因があって結果が生じたと因果律的に解釈されるとも言えます。
一応、サイコロはランダムな現象とされますが、厳密に空気抵抗や投げる力の強さ、角度等様々な原因の結果と考えれば、完全なランダムとは言えないという批判もあります。
また、カオス的な現象をもたらす力学系として、ロジスティック写像というものがあります。ロジスティック写像は、次の式で表される二次関数であり、パラメータと呼ばれる定数\(a\)が式中に含まれます。
\(y=ax(1-x)\)
ロジスティック写像は、次の状態が一意に決定するにもかかわらず、確率論的ランダムと同様、不規則な振る舞いをもたらします。そういった振る舞いはカオスと呼ばれます。
——————————————–(以下こちらより引用)
パラメータ a が a∞ = 3.56994… を超えると、ロジスティック写像はカオスと呼ばれる振る舞いを示す。カオスとは、大雑把に言えば、ロジスティック写像を表す差分方程式のように確率的な曖昧さがなく次の状態が完全に一意に決まるにもかかわらず起こる複雑で不規則な振る舞いのことである。ロジスティック写像の a > a∞ の範囲はカオス領域と呼ばれる。
——————————————–(引用ここまで)
ロジスティック写像は、以下のような不規則な挙動を示します。
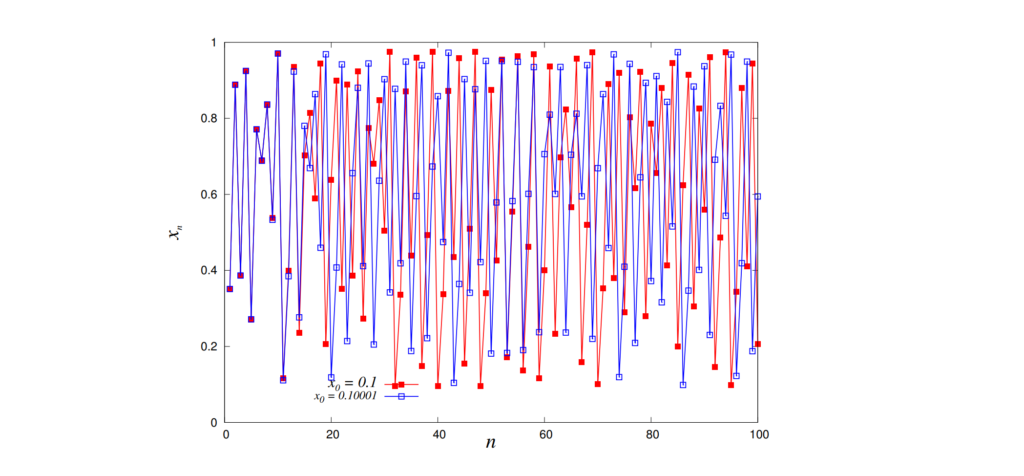
舞い.
ロジスティック漸化式とは、乱数表の乱数を生成するのに使われている数式です。とはいえ、乱数を生成するコンピューターも特定の関数で動いているため、完全なランダムを生成することはできず、「擬似ランダム関数」を用いているに過ぎません。
ここで、話を原子核の崩壊過程に戻します。
以前、原子核の陽子や中性子は、クォーク(=磁気単極子)によって磁力によってまとめられると説明しました。
◇原子核は「強い相互作用」「弱い相互作用」といった架空の力ではなく、磁力によってまとめられている。その確固たる証拠。(負の透磁率についてはこちら)
スミルノフ物理学によれば、陽子の場合は、N-S-N、中性子の場合は、S-N-Sの単極磁石で構成されているといいます。
原子核内は負の透磁率であるため、NとSは反発し、S極エーテル繊維はバネのような構造を持つため、中性子の場合、SS間でNが二点調和振動子として、振動します。
調和振動とは、理想的なバネにつながれて振動する物体の運動であり、調和振動子とは、質点が定点から比例する力を受けて運動する系のことです。
二点間ではランダムな振動ではなく、カオスによる決定論的な振動がなされており、xが0もしくは1のとき(つまり端点のNに到達したとき)、N極磁気単極子が正の透磁率下の外に飛び出し、中性子のS極磁気単極子を引き付け、原子核構造外へと運ぶことになります。
つまり、量子力学を始めとした現代物理学に則って、確率論なランダムな現象としてとらえられていた原子核の崩壊も、実際は因果律に基づいた決定論的な現象だったということになります。
具体的な数式で書くと、以下のようになります。
——————————————–(以下こちらより引用)
中性子を成すN極磁気単極子が
左端のS極磁気単極子から受ける右向き斥力は
F = k*x (1)
左端のSから距離1の位置に有る右端のS極磁気単極子から受ける左向き斥力は
F2 = k*(1 – x) (2)
となる。
運動が1サイクル完了する毎に、座標原点が1/2だけ右に移動して、その左右1/2、1/2の位置が新たなるS極磁気単極子の端点と成って行く過程を、数学的にモデル化する。
F1 = – k*x (3)
F2 = k*(1 – x) (4)
F1 + F2 = k{– x + (1 – x)} = k(1 – 2x) (5)
原点を1/2だけ右へ移動した後の座標をx’として
x’ = x – (1/2) (6)
x = x’ + (1/2) (7)
(7)を(5)に代入して
F1 + F2 = k(1 – 2x) = k{1 – 2(x’ + (1/2))} = 2k*x’ (8)
今、対数関数については
ln X*Y = ln X + ln Y (9)
なる関係式が成り立つ。
又、
(ln Z)’ = 1/Z
Z = 1の時
(ln Z)’ 「Z=1」= 1/1 = 1
であるから(0, 1)の区間に於いては、概算として
Ln Z ≃ –1 + Z = Z – 1 (10)
と表せるから、これを基に
ln F1*F2 = ln F1 + ln F2 (11)
を考える。
(0, 1)の区間では概算
F1*F2 ≃ F1 + F2 (12)
(8)を使って
F1*F2 ≃ F1 + F2 = 2k*x‘ (13)
(3)、(4)
F1 = – k*x (3)
F2 = k*(1 – x) (4)
を(10)を考慮して(13)の左辺に代入して
–k(1 – x)*k{1 – (1 – x)} ≃ F1*F2 = F1 + F2 = 2k*x‘
k^2*x(1 – x) = 2k*x‘
k*x(1 – x) = 2*x‘ (14)
ここでk=8と置くと
8*x(1 – x) = 2*x‘
4*x(1 – x) = x‘
x‘ = 4*x(1 – x) (15)
此処に安定な1次元非線形決定論カオスを表すロジスティックス漸化式を得る。
不定値kの式(14)の段階でも変動する不安定なロジスティックス漸化式を表している。
原子核内S-N-S構造の中性子のN極磁気単極子が、通常は安定な2点間調和振動子のロジスティックス決定論カオスに落ち着いているのは、公転軌道関係に入った時にフックの法則が公転軌道安定化の為に働くのと同じく、バネとして働くソレノイド型のS極系エーテル繊維が安定性を求めて固定点間の長さを調整する合目的的反エントロピー的特性を有しているからである。
この2点間調和振動子の構造は数学的にはテンソルとして定義される。
テンソルの一般的定義に基づき、直線座標の1次元空間に隣同士2種類の座標系(xi)i、(x’i)iが与えられていて、それらの間の関係が行列
A = (aij) (16)
を用いて
x’i = (i = 1~d)Σaij*xj
と表される。
隣同士2種類の座標系(xi)i、(x’i)iとは、ここでは始め左端S極磁気単極子の位置を原点0とした座標系が(xi)jであり、原点を1/2だけ右に移動した後の座標系が(x’i)jである。
具体的には
行列Aを
Matrix | 1 1 |
| –(1/4)λ 0 | (17)
なる構造を持った2点間調和振動子を表すものとして定義し
A * X = λ* X (18)
なる式で固有値、固有ベクトルを求める。
A – λI = Matrix | 1 –λ 1 |
| –(1/4)λ -λ | (19)
Det | 1 –λ 1 |
| –(1/4)λ -λ | = 0 (20)
行列式の方程式(20)を解いて
– (1 – λ)λ = -(1/4)λ’
λ = 4λ(1 – λ) (21)
λの値が漸化式にダイナミックにフィードバックされて行く為に、左辺のλをλ’に置き換えて
λ’ = 4λ(1 – λ) (22)
此処に再び式(15)と同じ1次元非線形決定論カオスを表すロジスティックス漸化式を得た。
(21)の2次方程式を解いて固有値、固有ベクトルを求めると
4λ^2 – 3λ = 0
λ(4λ – 3) = 0
を解いて
固有値はλ= 0 又は 3/4
固有値λ= 0の場合
Matrix | 1 1 | * vector |x1| = Vector |0|
| 0 0 | |x2| |0|
x1 + x2 = 0
0*x1 + 0*x2 = 0
x2 = –x1
よってこの場合の固有ベクトルは
Vector | 1 |
| –1 |
固有ベクトルが1と–1を2成分とするのは、2点間調和振動子N極磁気単極子が常に左・右の両端のS極磁気単極子からそれぞれ正の方向の右向き・負の方向の左向き(順不同)の力を受ける事を表している。又固有値が0であるのは、調和振動子である事を表している
固有値λ= 3/4の場合
Matrix | 1/4 1 | * vector |x1| = Vector |0|
| –(3/16) –(3/4) | |x2| |0|
(1/4)*x1 + x2 = 0
–(3/16)*x1 – (3/4)*x2 = 0
–4*x2 = x1
よってこの場合の固有ベクトルは
Vector | –4 |
| 1 |
固有値3/4の場合、更に固有ベクトル
Vector | x1 |
| x2 |
を固有関数と考えて、固有関数を求めると、
x1 = 4*x(1 – x) – x
x2 = 0
と置くと
再び
x = 4*x(1 – x)
これをダイナミックな漸化式に書き換えて
x‘ = 4*x(1 – x)
1次元非線形決定論カオスを表すロジスティックス漸化式を得る。
此処に2点間調和振動が一見ランダムに見えるが、実は確率過程ではなく、ロジスティックス漸化式による非線形1次元決定論カオス振動を成している事が論証された。
普遍的に言って、「放射性元素原子核の崩壊が一見ランダムに見える」事が実は確率過程ではなく、ロジスティックス漸化式による非線形1次元決定論カオス運動であり、一見予期せぬ時点でx = 0またはx = 1となった瞬間、端点のS極を越えてN極磁気単極子が無限大斥力を受けて外に飛び出し、次の瞬間、正の透磁率の世界に出たN極磁気単極子は中性子を成しているS極磁気単極子を引き付けて原子核構造から外へと運ぶこととなる。
此処に、現代量子力学が確率論を持ち込む誤りに陥った主要な動機である「放射性元素原子核の崩壊が一見ランダムに見える」事が実は確率過程ではなく、ロジスティックス漸化式による非線形1次元決定論カオスである事が論証された。
——————————————–(引用ここまで)
つまり、私たちの生活する物理世界は、確率論に基づいたランダムな世界ではなく、明確な原因と結果の因果律に基づいた、決定論的な世界であると言えます。
私たちの身の回りに起きることは、偶然ではなく必然だと言えるかもしれません。
見よ、この事はわが前にしるされた、「わたしは黙っていないで報い返す。そうだ、わたしは彼らのふところに、 彼らの不義と、彼らの先祖たちの不義とを共に報い返す。彼らが山の上で香をたき、丘の上でわたしをそしったゆえ、わたしは彼らのさきのわざを量って、そのふところに返す」と主は言われる。
イザヤ書 65:6-7
念のため、放射線自体、単なる磁気単極子(つまり電磁波)に過ぎず、つまるところ危険ではありません。
◇「CTスキャンで癌になる」というミスリード。癌は存在せず、放射線はただの電磁波である。
情報に溢れるこの時代で、確固たる真理を基に嘘と本当を見分ける必要性があります。私は、RAPTブログを学ぶことで、真実と嘘・偽りをはっきりと見分けることができ、マスコミやSNSにおける悪質なミスリードを避けて、安全に、幸福に生きてきました。
一人でも多くの方々が、RAPTブログを学び、真実を見分け、幸福に生きられますことを心よりお祈り申し上げます。
お読みいただきありがとうございました。










コメント