はじめに:見えている“傾向”は本物か?
現代のデータ分析では、よく「移動平均(Moving Average)」を用いる手法が使われます。
この手法は、時間の経過に沿ってならぶ、元のデータに対し、”フィルター”として、「移動平均」を取って、データの背後にある「傾向」を浮かび上がらせることを目的としています。
たとえば、売上や株価などの時系列データにおいては、「ノイズ(短期的なバラつき)を消して、トレンド(長期的な傾向)を見たい」という目的から、移動平均を取って滑らかなグラフを描きがちです。
たとえば、毎日激しく変動する株価データに対して、直近の一定期間(例:5日間)の終値の平均を求め、それを折れ線グラフとしてプロットしていくと、日々の小さな変動が抑えられ、全体の傾向や流れが視覚的に捉えやすくなります。これを単純移動平均といいます。
しかし、それは本当に“傾向”を捉えているのでしょうか。
もし、統計学者自身が、データに様々な処理を施すことで、存在しない傾向を“捏造”してしまっているとしたら——
スラツキー効果とは?
この問いに大いに関係するのが、1920年代に、ソヴィエト連邦の数学者・経済学者「エヴゲニー・スルツキー」によって発見された「スラツキー効果(Slutsky effect)」と呼ばれる現象です。

「スラツキー効果」は、完全ランダムなデータでも、移動平均などの処理をすると周期性やトレンドがあるように見えてしまうというものです。
すなわち、
ランダムなデータに移動平均処理を施す
→見かけ上の周期性やトレンドが生まれてしまう
→ 実際には存在しない「傾向」を人間が錯覚してしまう
つまり、完全に無秩序なデータでさえ、移動平均をかければ“それっぽい波や流れ”——周期性が現れてしまうのです。
例えば以下のような、一様にランダムなデータ50個も、
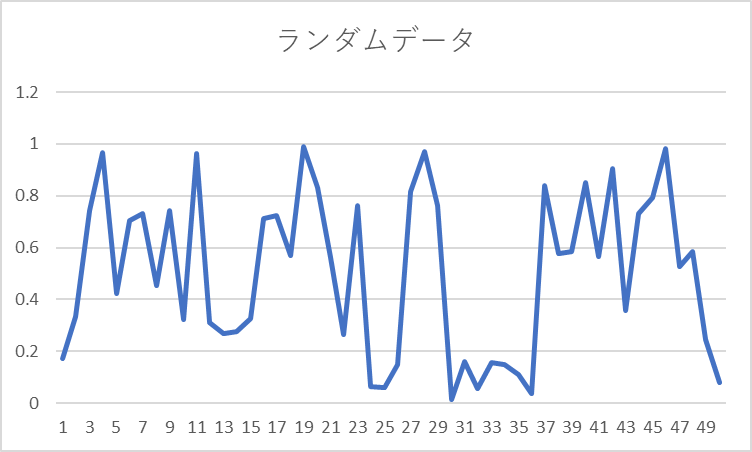
以下のように、単純な移動平均(5個ずつの移動平均)を取ることによって、一見すると、上下に繰り返す、特定の傾向があるように見られますね。
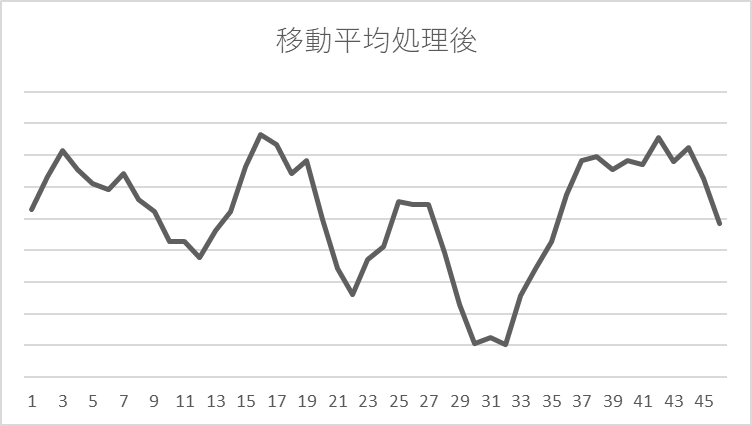
移動平均を取ることによって、一定の周期性が、この完全ランダムなデータからもたらされてしまうのです。
このように、周期性を”作り出してしまう”のは、「移動平均」だけではありません。
最近のデータに重みを置いて平均化する「指数平滑法」や、特定の周波部分をノイズとしてカットし、特定の周波をトレンドと見なす「フーリエフィルター」などといった、あらゆる統計的処理を含みます。
つまり、時系列データを滑らかにするすべての統計的操作に「スラツキー効果」によるリスクが潜んでおり、統計学者たちがデータに施していた処理によって、本来はあるはずのない周期性や振動を、意図せず”捏造”してしまっていたことが明らかになったのです。
現代のデータ分析に潜む危うさ
データ分析では、当たり前のように、
- 株価の移動平均をとってトレンドを読み取る
- 売上にスムージング処理をして傾向を探る
といった操作を行います。
しかしこれは、真の傾向を見ているというより、スラツキー効果によって作られた“幻影”を見ている可能性があるのです。
そう考えると、多くの「トレンド分析」は、統計の皮を被ったエセ科学になる危険性があります。
株価予測で移動平均を使うリスク
多くの投資家やアルゴリズムは、過去のデータに移動平均をかけて「上昇トレンド」や「サポートライン」を読み取ります。
しかし、スラツキー効果の観点からすると、それは無作為な変動に“意味”を読み込んでいるだけといえるでしょう。

本当に予測したいなら「構造」を見るべき
では、どうすればよいのでしょうか?
これまで見てきたような、単なる平均処理ではなく、データの背後にある構造や因果関係をモデル化する方法が必要です。
GMDH(多項式モデル)というアプローチ
本当に時系列で並ぶデータにおける「因果関係」や「内部構造」を知りたいのなら、ただの移動平均ではなく、構造的なモデル化が必要です。
たとえば、以前のブログでも紹介したように、GMDH(Group Method of Data Handling)のような多項式モデリング手法が有効です。
◇ディープラーニングは本当に「学習」しているのか──GMDHに見る学びの本質
GMDH(Group Method of Data Handling)は、データの関係性を多項式の形で表現することで、
「和」や「積」による「構造的な因果のモデル化」を目指します。
多項式は、足し算や掛け算の組み合わせでデータの複雑な構造を表すため、
そこから、因果関係に近い重要な関係性を見つけることができます。
これは、単純に「データをならして傾向を探す」のではなく、
データの中に隠された生成メカニズムを、「関数を抽出する」ことによって発見するアプローチです。
この方法なら、「平均で捏造された傾向」ではなく、「データが語っている本質的な動き」に近づける可能性があります。
そもそも、データのノイズ(不規則な振動)は、本当に雑音なのか、それとも関数で表せて、擬似乱数を生成するカオス数列のような意味のあるデータなのか、単純な統計的処理では見分けることが難しいのではないでしょうか。
そういった意味でも、多項式によって因果関係を明確にするGMDHのような仕組みは、有用なのではないかと考えられます。

まとめ:見かけの”傾向”から、ソリッドな”因果構造”へ
見えているのは“傾向”ではなく“錯覚”かもしれない
ここまでみてきたように、具体的な株価予測や売上予測に移動平均を使うと、スラツキー効果により“幻想のトレンド”を生みかねません。
ランダムなデータにすらトレンドを“生じさせてしまう”移動平均”をはじめとした統計処理。それに無自覚なままトレンドを語ることは、科学的ではないと言わざるを得ません。
データに隠れた因果関係を見出すには
繰り返しになりますが、ノイズを滑らかにするだけでは、完全な予測にはなり得ません。統計的な相関関係は、1つの判断材料にはなるかもしれませんが、因果関係そのものを証明するものではありません。
ですから、データをきちんと読み取るためには、根本的な因果構造のあるモデリング(GMDHなど)が、より信頼できる分析に繋がるのです。
見かけのデータの滑らかさや傾向を見出すことに惑わされず、本質的な「構造」や「因果」に踏み込む必要があります。多項式モデル(GMDHなど)はその一つの道になると考えます。
お読みいただきありがとうございました。











コメント