はじめに
近年、ディープラーニングはAIの中核技術として急速に発展し、画像認識や自然言語処理、音声合成など、さまざまな分野で目覚ましい成果を上げています。
このディープラーニングの中心にあるのが「ニューラルネットワーク(NN)」と呼ばれる仕組みです。人間の脳を模したこの計算モデルは、膨大なデータを元に自動で特徴を抽出し、学習を進めていくことが可能とされています。
しかし、ここで立ち止まって考えてみたいのは、「本当にこれは“学習”と言えるのか」という問いです。
私たちが学ぶとき、それは単なる記憶や暗記ではなく、「なぜそうなるのか」という仕組みやルール、つまり関数的な関係や法則性を理解するプロセスのはずです。
ところが、現在のディープラーニングの多くは、関係性の理解ではなく、「膨大なデータを用いた最適な“パターンの記憶”にとどまっている」のではないでしょうか。
今のAIは「覚える」のが得意
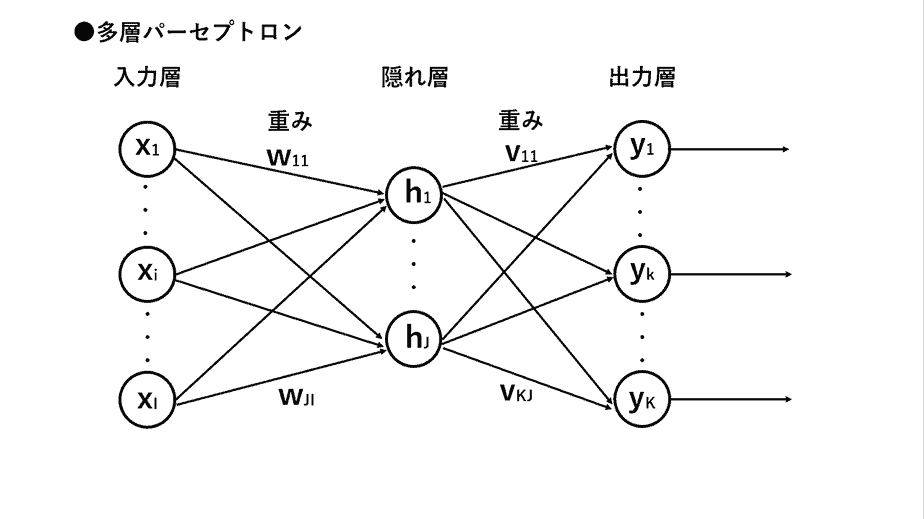
現在のAI(特にニューラルネットワーク)は、図1に示したように、「多数の数値(重み)」を使って情報を処理しています。これは、端的に言えば「うまく計算してパターンを記憶する」ような仕組みです。
つまり、ニューラルネットワークは、入力と出力の関係から統計的なパターンを学習します。これは人間のような「意味の理解」とは異なり、むしろパターンの記憶と再現に近いものです。
たとえば、画像や音声といった大量のデータを読み込み、「これは猫に近い」「これは音楽っぽい」といった判断を下します。しかし、それは本当に理解と呼べるものでしょうか。 単なるパターン認識=記憶にとどまってはいないでしょうか。
このように、現在のAIの多くは、「意味」や「文脈の理解」ではなく、データ上の類似性や確率的な傾向に基づいて判断を下しているのです。
現在のニューラルネットワークの仕組みとその限界
今、主流となっている人工ニューラルネットワークは、基本的にとてもシンプルな構造をしています。核となるのは2つの処理です:
- 重み付きの足し算(線形結合)
- 活性化関数による非線形変換
まず、入力に対して「どの情報をどれだけ重視するか」を決めるために重みをかけて足し算します(これが線形な処理)。そのあとで、ReLU(ランプ関数)やシグモイド関数のような単純な非線形関数を通すことで、「直線的な計算」では表現できない複雑な関係をモデル化しようとしています。
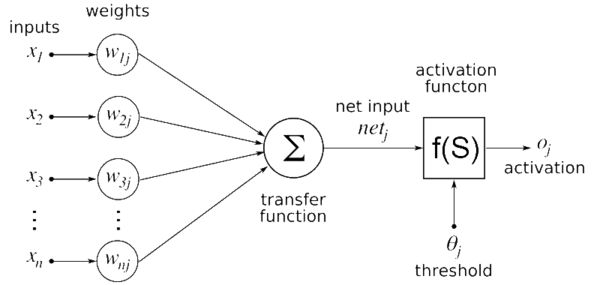
この仕組みは非常に強力で、画像認識や自然言語処理のような高度なタスクでもうまく機能しています。ですが、一つ大きな問題があります。
この構造だけでは、任意の関数の形を完全に自由に表現できるわけではありません。
なぜなら、線形な組み合わせはどこまでいっても「直線的な計算」にすぎず、そこに「非線形性(ゆがみや曲がり)」を加える唯一の方法が、ReLUなどの単純な関数に依存しているからです。
したがって、この構造では、本来必要な「任意の関数形」を柔軟に扱うことができません。
そこで一たび原点に立ち返って、本質的な「学習」とは何か考えてみましょう。
本当の「学習」とは何か
本来、「学ぶ」というのは、「なぜそうなるのか」「どういう仕組みか」を理解することです。
つまり、「関係性」や「法則」=関数を見つけ出すことが、本当の意味での学習です。
数学の世界では、どんな複雑なルールも、「多項式」という形で近づける(近似する)ことができます。
たとえば、
- y=2x+1y = 2x + 1y=2x+1(直線)
- y=x2−3x+2y = x^2 – 3x + 2y=x2−3x+2(曲線)
こんな形で、世の中のルールを数式として表すことができるのです。
学習とは「関数の抽出」である
真の意味での「学習」とは、データの中にある関係性=関数そのものを抽出することだと言えます。
任意の関数は、マクローリン展開やテーラー展開によって多項式の形に展開可能であるという数学的性質があります。
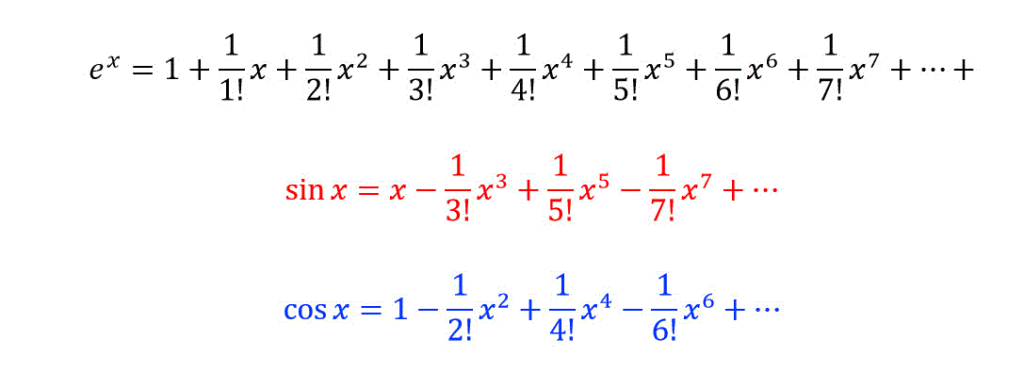
つまり、「どんな関数でも本質的には多項式で近似可能」だとすれば、線形な重み付き”足し算”しか扱えない現在のニューラルネットワークのような構造ではなく、掛け算も扱える多項式を使って学習する構造のほうが理にかなっているのです。
GMDH:関数を見つけるためのニューラルネット
1968年にソ連の科学者アレクセイ・G・イヴァフネンコ(Alexey G. Ivakhnenko)によって開発された「GMDH(Group Method of Data Handling)」は、まさに「多項式モデルによる学習」を実現するための手法です。

GMDHは、入力データに対して多様な多項式モデルを自動的に生成・評価・選択し、最適なモデル構造およびパラメータを帰納的に導出します。
「GMDH(ジー・エム・ディー・エイチ)」という手法は、まさに「関数=法則」をデータから自動的に抽出することを目的とした人工知能の一形態と言えます。
GMDHは、複数の数式モデルを試行し、その中から最も適合度の高いものを選択する仕組みを備えています。すなわち、単なる記憶ではなく、
「この現象は、どのような数式で記述できるか?」という視点から自律的にモデルを構築していくのです。
これは、「データの記憶」や「確率・統計的処理」にとどまらず、関数そのものを発見することを目的としたアプローチであると言えるでしょう。
なぜ今、GMDHが再び注目されるべきか?
現在のディープラーニングは、何百万、何千万というパラメータを使って、データの特徴を圧縮・記憶する能力には優れています。
しかしその多くは、「関数の抽出」ではなく、分類や識別の最適化=データの再現に近い処理になっています。
結果として、ニューラルネットワークは次のような問題点があります:
- モデル構造がブラックボックス化しやすい
- 本質的な因果関係を捉えることができない
- 「なぜそうなったか」が説明できない
- 膨大なデータを与えないと学べない
こうした課題に直面する今こそ、「法則を見出す」という学習の本質に立ち返るべきではないでしょうか。
GMDHは、まさにその視点を内包した手法です。データの背後にある因果的構造を明示的に捉えようとするこのアプローチは、現行のニューラルネットワークよりも、人間の学習・推論プロセスに近いものと考えられます。

まとめ:GMDHの再評価を
人間の学習とは、単なる記憶の蓄積ではなく、「なぜそうなるのか」という因果関係を理解する過程にほかなりません。
このように、構造と関係性の理解、すなわち「関数の抽出」に基づくAIの学習こそが、本来あるべき姿ではないでしょうか。
この観点から見ると、GMDHの多項式モデルは、従来のニューラルネットワークに比べて、より理論的に洗練された学習形態を提供していると言えます。
確率的・統計的な処理に依存する現在のニューラルネットワークとは異なり、因果関係を明示的に説明可能な多項式を用いるGMDHは、人間の推論システムにより近いアプローチであると考えられます。
1968年に提案されたGMDHは、「理解するAI」を目指した先駆的な試みであり、半世紀以上を経た今、その価値をあらためて見直す意義があるのではないでしょうか。
最後までお読みいただき、誠にありがとうございました。











コメント